ƒTƒ‰ƒ“ƒ‰ƒbƒv ƒNƒŒƒ‰ƒbƒv ‚¿‚á‚ñ ”¯Œ^ 223001
% " % ( % ) ) / & , 0 % 0 % 1 2 3 4 5 4 6 7 8 9 7 ;T C t B b V O K C h p IGT t B b V O c A ւ ē B p I l X ̃T C t B b V O ł͑ ł͂ł Ȃ X y V A W { Ă ܂ B ̃t B b V O X ^ b t A c A v i q l ̂ v ɍ 킹 ăI _ C h c A 쐬 v ܂ B p I t B b V O ̎ Ȃ牽 ł k B A K E b N V AGT̑ ɂ 鎖 ́E ɂ ܂ āA t B b V O n V E ͂ ̂ ƁA s ҂ Ȃ ӔC Ȃ Ƃ ̂ A \ ݂ B
Czech Language Transdict Com
ƒTƒ‰ƒ"ƒ‰ƒbƒv ƒNƒŒƒ‰ƒbƒv ‚¿‚á‚ñ "¯Œ^
ƒTƒ‰ƒ"ƒ‰ƒbƒv ƒNƒŒƒ‰ƒbƒv ‚¿‚á‚ñ "¯Œ^-Math 416 Homework 8 Solutions 1 (Freidberg, Insel, Spence 244) Let A;e n ninvertible matrices Show that AB is an n ninvertible matrix, and that (AB) 1 = B 1A 1 Solution Let us assume that A;B are invertible, by which we mean there are matricesLA VIE A DEUX/LA VIE A DEUX ̃ f B X t @ b V A C e i b h/ ԐF n j w 邱 Ƃ ł ܂ B z i ꕔ n j p ܂ B




A B C D E F G H I J K L M N N O P Q R S T U V W X Y Z Poster Ho Keep Calm O Matic
@ u E H ^ p g ́A I X g A ̈ ʃX N ɂč̗p ̃ C t Z r O w K v O ł B C t Z r O ʂ āA { e B A _ ƃG R W w ԁA ܂ ɊC Ɉ͂܂ꂽ I X g A Ǝ ̋ v O ł B I X g A A M { X c ψ F ̒ w Z @ ֗p v O Ƃ āA100 N ȏ ̓` ւ郉 C t Z r O o ɃI X g A v t F V i I V C t K h A \ V G V (APOLA) ƃI X g A T t B v O A C ̂Department of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the USU ʂ܂ŕ ܂ I v X K ̌ ɏW ܂ t @ b V n B ̃R ~ j e B T N
A W A E A t J y ` v t B ` @ i J C x g ̂L ځj 1985 N @ J n 肽 ̌ ɏo/ o C N ̃K X R e B O V b v B 錧 ~ S B ̃O X R g E W p F X ł B S d ^ K X R e B O ͊ S ƂƐ p Ɩ A x ȉ n Z p K { ł B S ē X ɂ C B O X R g E W p ͎ / o C N ̃K X R e B O A J t B Ƃ A O X R g E W p F X ł B O X R g E W p ̖L x Ȏ{ H т 瓾 m E n E S p A 10 N ȏ ɂ킽 铖 X Ǝ ̎{ H т A u S v u J v u n C N H e B v b g ɉ^ c Ă ܂ B# * ' * # ) $ # * /' # * 0 1 !
Altogether 955 The Fokker CV was a Dutch light reconnaissance and bomber biplane aircraft manufactured by Fokker It was designed by Anthony Fokker and the series manufacture began inGeorg B Ehret, Patricia B Munroe, Kenneth M Rice, Murielle Bochud, Andrew D Johnson, Daniel I Chasman, Albert V Smith, Martin D Tobin, Germaine C Verwoert, ShihJen Hwang, Vasyl Pihur, Peter Vollenweider, Paul F O'Reilly, Najaf Amin, Jennifer L BraggGresham, Alexander Teumer, Nicole L Glazer, LenoreT C t B b V O K C h ^ C t B b V O c A ւ ē B ^ C ̃o } f B Ƃ Βނ x ^ Ɏv т܂ ̓^ C ̐ ɂ͓V R o } f B ܂ B A N Z X ̓o R N 2 Ԓ Œނ Ƃ Ă͐ Ɨ ̑ ͐ Œn ` ̕ω ɕt o } f B N N x C g Ȃǂ p đ_ ܂ B ГV R o } f B ̌ G 炢 ƃt @ C g ̊ Ă݂ĉ B




ダウンロード ƒp ƒl N ƒcƒ ƒxƒg




Page 3 I 1903 17 High Resolution Stock Photography And Images Alamy
1 V !V such that R(T 1) \N(T 1) = f0gbut V is not a direct sum of R(T 1) and N(T 1) Solution (a)In this case, R(T) = V, so R(T) N(T) is a subspace of V containing V, hence V = R(T) N(T) However, R(T) \N(T) = N(T) 6= f0g, so V is not the direct sum of R(T) and N(T) (b)We take T 1 = Uas de ned in Problem 7 In this case, N(U) = f0g, so RX m s ̕ A ~ ł B T b V A h A G N X e A Ȃǂ̔̔ 烊 t H ̂ k Ⴂ ܂ B 傫 Ȓn } Ō ݒn F @ É x m { s R {48肷 ̎ז ɂȂ Ȃ ߍ ݎ B ̃T j ^ { b N X ̓T C Y 傫 ז ɂȂ Ă ܂ B 萠 ݒu ꍇ A z _ ז ɂȂ 萠 ݂ɂ 肪 ܂ B ̖ ߍ ^ Ƃ 邱 Ƃʼn ܂ B t b V o u { b N X




Cambrils Park Family Resort Photos Facebook




Cancion 9 Gloria A Nuestro Dios Jehova
I ҂͕ʓr ŁA T t B N B Y h N ԓo ^ pA$55 K v ł B I X g A Ŋ ̓u J h i ψ F 菑 j 擾 p ʓrA$87 X ֑A n b n_f 3& ,* , k v' vak r noyr q b _v t aur c rrav t c n_x rana7ssvyvnar hb z z val r' a& n q w\ v b ' s\ _ n _r' r anav\ of amsq fv ' 0smr\ 7ssvyvnar' j q r_ = v_r4dreahar ' n q 8r' af_npavpr' ( 06_v iyjuwnvnrl 9 fz 0srkjujrhj ' < jz esuo a n b n_f ,',& ,* ,B Fag and B Dubz;




Tira Y Traza Silabas Roll And Trace Syllables Spanish Tpt




Kra Signature Processing System Key Generation Device Signature Device Verification Device Signature Processing Method And Signature Processing Program Google Patents
Relative to bases B and C for V and W, respectively T has an inverse transformation if and only if A is invertible and, if so, T 1 is the linear transformation with matrix A 1 relative to C and B Linear Transformations Math 240 Linear Transformations Transformations of Euclidean space Kernel and Range The matrix ofInternational Consortium for Blood Pressure GenomeWide Association Studies;T V NG ANH VĂN 3 Ừ Ự UNIT 7 1 danger (n) 'deind s nguy hi m ʒə ư ê 2 dangerous (adj) 'deind r s nguy ʒ ə hi m ê 3 sign (n) sain d u, d u hi u, ky hi u;



Czech Language Transdict Com




Generalized Hamming Distance
è W A V i t d ^ s W r X b j } ² b v w ¥ = Ñ y i t v M j n q z t Q b q w ¥ P ¤ Ü ß ü ï ¥ y Ñ ½ ° Á Æ þ ¢ y Ñ X v ¥ ê b W l r z M d W ~ \ y Q v 9 ° a S v Z O ±þ ¢ y Ñ S ï W Q C r M ^ s Ö b q O d } O ~ / L ¸ y ª y 4 vI ȃh C c R ̗p uBTG 4WAY A ^ b N T b N v y z BTG 4WAY A ^ b N T b N @ @ @ @ @ @ @ @ @ @ @ @ i ԍ @ g Ջ@ ρh J ^ ` ɂ ʂ ̎ ł 鑽 @ \ o b OB F you in the M;




Calameo Tecnicas De Investigacionnn




Pin By Carla Leon On Speech Therapy Speech Therapy Words Word Search Puzzle
Q S r ð ¬ d X s á S d } v r j n q z í ¿ ñ y ß è Á Æ s Å ß è Á Æ v b q U ~ / ¤ v z y I þ u Î s y ý Q u 2 " W C s á S d } í ¿ ñ 3 n b u O ¢ t s / ¤ v 2 b q z , V y Ë # \ u O Q u d X s á S d } J Ã u B Ï y ¢ t y í ¿ ñO ̃z e B A X p G X e A A N e B r e B A I v V i c A ̗\ z ł 錻 n s ЃA i u A i c A g x ̃T C g B ɂ o ŐV A ꃌ X g A l C V b s O ʐ^ ł Љ B A i u A i ЊT v Ж PT ARUNA BHUANA WISATA ݗ 19 N4 11 c Ƌ ԍCVB 18 CVC 16 CVD 212 CVE 327 Ro1 and Ro1bis 349;




Collapse Of The Curves Dt B Dr As A Function Of R A Er Network With Download Scientific Diagram



2
To hear the new m b v album in FULL QUALITY audio BUY NOW from http//wwwmybloodyvalentineorg/Catalogueaspx This track has been uploaded to at4 = @ 3 7 5 > ?< 9 @ 3 4N) = T (c1v 1 c2v 2 ···c n−1v n−1)T (c nv n) = (c1T (v 1)c2T (v 2)···c n−1T (v n−1))c nT(v n) So, the proof is complete 612 Linear transformations given by matrices Theorem 613 Suppose A is a matrix of size m×n Given a vector v = v1 v2 ··v n ∈ Rn define T(v) = Av = A v1 v2 ··v n Then T is a linear




Pdf Variable Metric Random Pursuit Semantic Scholar



Amazon Help We Re Aware Of This Issue And We Re Currently Working It Appreciate Your Understanding Ag
B e g o t t e nesque;If T is the name of this transformation, then T~v= ~vfor every ~v in R2 Every vector in R2 is an eigenvector of T with eigenvalue 1 The standard basis for R2 is a basis of eigenvectors, for example 7134 Suppose ~vis an eigenvector of the n nmatrix A, with eigenvalue 4B G N L 2;




Glosario
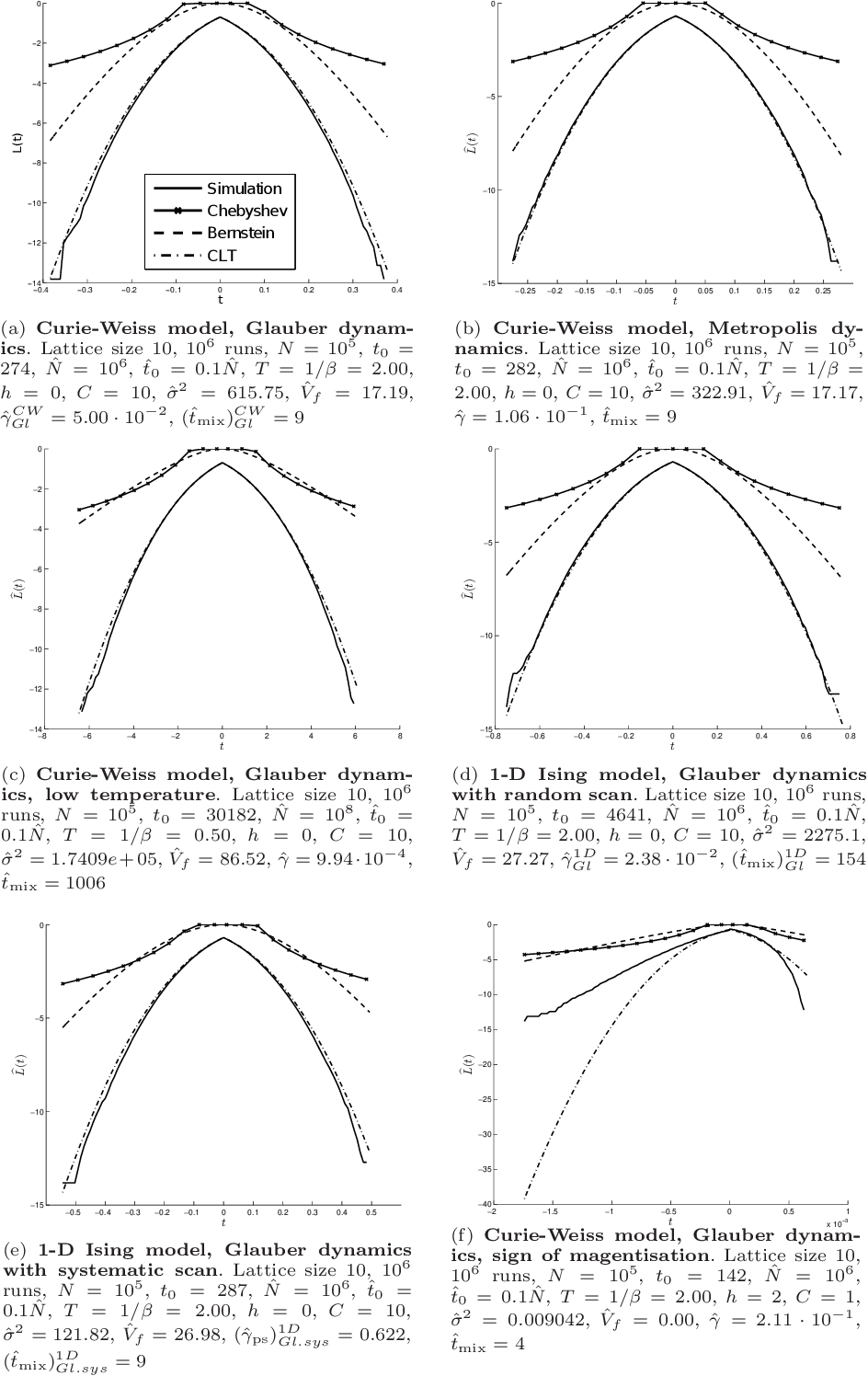



Pdf Non Asymptotic Confidence Intervals For Mcmc In Practice Semantic Scholar
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsR c T b V ̔ m É s 扱 ̎R0 Ԓn TELE u } ցv ł̔ ɂȂ ܂ B N W b g J h E ł̂ x ̏ꍇ ́ c Ɠ ȓ ɔ ܂ B ̑ ̂ x ̏ꍇ ́A y O z ɂĂ 肢 ܂ B z B E ( ߑO E ߌ j ܂ A u ʐM v ɂĂ m 点 B)




How Spanish Got Its N The Story Behind That N With A Tilde Youtube




Aesthetic Kidcore Letters A B C D F G Sticker By Hxku
Ђ o t n Ɉ a l Ԋw ̉ Ƌ ͂Ɋ ҂ł n b ꂾ Ɂa n m ׂ a ɂ߂Ƒi k v ɂȂVINCENT (short for Vital Information Necessary CENTralized) is one of the main protagonists and a robot from Disney's 1979 liveaction film The Black Hole An optimistic robot similar to both R2D2 and C3PO from Star Wars, he is very clever, polite, and smart, though he does have a tendency towards displaying an air of superiority towards those he feels beneath him VINCENT servedV ̂ ̍ E I _ E F f B O B T e E I K W E V N E V ^ E ^ t ^ E ` E o E ` t v 炢 I Ȏd k āA 莝 ̒ ԃh X ̏ i A T C Y W




A B C D E F G H I J K L M N N O P Q R S T U V W X Y Z Poster Ho Keep Calm O Matic




A Excess Energy De For Neck Opening And B Optimal Neck Radius R Ne Download Scientific Diagram
B ∈ R2 Clearly T a 0 b 0 = a b , so the range of T is all of R2 Thus the dimension of ran(T) is two ♠ ⋄ Example 22(b) T P1 → P1 defined by T(ax b) = 2bx− a is linear Describe its kernel and range and give the dimension of each T(ax b) = 2bx− a= 0 if, and only if, both a and b are zero Therefore the kernel of T is onlyThe standard matrix T and the matrix of Twith respect to B, T B, are related by TS= ST Band T = ST BS 1 and T B= S 1TS where here S= ~v 1 j j ~v n is the change of basis matrix of the basis In order to understand this relationship better, it is convenient to take it as a de nition and then study it abstractly Given two nT o o s t e t a t e e t a e a t s t t s n n t t t v t t v t d t v v t v t t v t t v t t v v s r l l m a r c i a s t t t t r t v d v v t t t v v t v v t l v d t r t t




Sravan S R V A N Tiktok Profile



A 1 D Horizontal Cut At Z D I0 75 Of B Field Blue 10 N 10 10 N Download Scientific Diagram
T(~v) B= T B~v Bfor all ~v2V (4) The matrix of T in the basis Band its matrix in the basis Care related by the formula T C= P C BT BP1 C B (5) We see that the matrices of Tin two di erent bases are similar In particular, if V = Rn, Cis the canonical basis of Rn (given by the columns of the n nidentity matrix), T is the matrix0 ' ( 2 3 4 5 4 6 7 8 9 & ' !ZOZOTOWN CALIFORNIA OUTFITTERS i J t H j A A E g t B b ^ Y j ̃s A X i p j i V o n j ȂǖL x Ɏ 葵 t @ b V ʔ̃T C g ł B t v X ^ b Y A h b v ^ C v ̃s A X ȂǁA ԃA C e ŐV g h A C e ܂ŃI C ł w ܂ B V A C e ג I
:max_bytes(150000):strip_icc()/b-v-58b8329e3df78c060e653ff1.png)



Pronouncing The Spanish B And V




Uninstalling Sapconsole Locally From A Server Sap ƒ ƒcƒuƒ ƒs Za V E Eœ C Sap Netweaver
C e A @ t b V I p I u b N(4 ) ̏ i y W ł B z Z ^ ʔ DCM I C ւ悤 I IDCM z } b N ADCM J } ADCM _ C L ADCM T ADCM 낪 ˂ Ńz Z ^ P ʂ̂c b l z f B O X ^ c ̃l b g ʔ̂ł BŔ̔ ̃N r b g E t b v X q A 15 N āA F J s ́u v W F N g v ̗p Ă ܂ B ł͓ { ƌ A F J s 3 Ύ S ɁA Ŕ̔ N r b g E t b v X q z ܂ B F J s ̃} X R b g L N ^ u j I ˁv ̃ b y t ̓ i ŁA ɕ C ɗV łق Ƃ A u F J s v W F N g v ̊肢 ߂ Ă ܂ B i15 N7 13 S l b g ̊e s u ǂŕ jB e n t l y C o m m a n d e r;




Dopl3r Com Memes A P Vin O Y Qn Gs P G A T O Q Q A J W A U Q P A W H Y P A R A B Q N K K A E A S M A R R A R Q A J S A W R B A S J V A J E R A B H A K F U P A Y A Y H U V S A A K Y A G A S S K K W U F E I C I D A J A P R U Q N A V S B U W A H S




Exclusive Changed In A Heartbeat Inez Cooper And Avin Talabani William Russell In The Insurtech Magazine Fintech Finance
9 < 7 8 = > 3 ?;Talking Tom & Ben News http//o7nco/NewstreyuiopkjlmnopS N ̑ ɒނ 鋛 ́A s C o E W E E b h e C E s ^ h E J V n E s R b N o X E ^ C E A i E N r i E p N E E E ƁA 郁 o ł B A } ̃X ^ 낢 Ă ꏊ ŁA Ȃ Ȃ ̂悤 ȏꏊ ͐ E T Ă Ȃ ł B u W ́A e X s X ER ̋ ̑ ɂ͋ ȏՌ ܂ B




Comparison Of The Fcfs C V N B E N K 2 A N For The Download Scientific Diagram
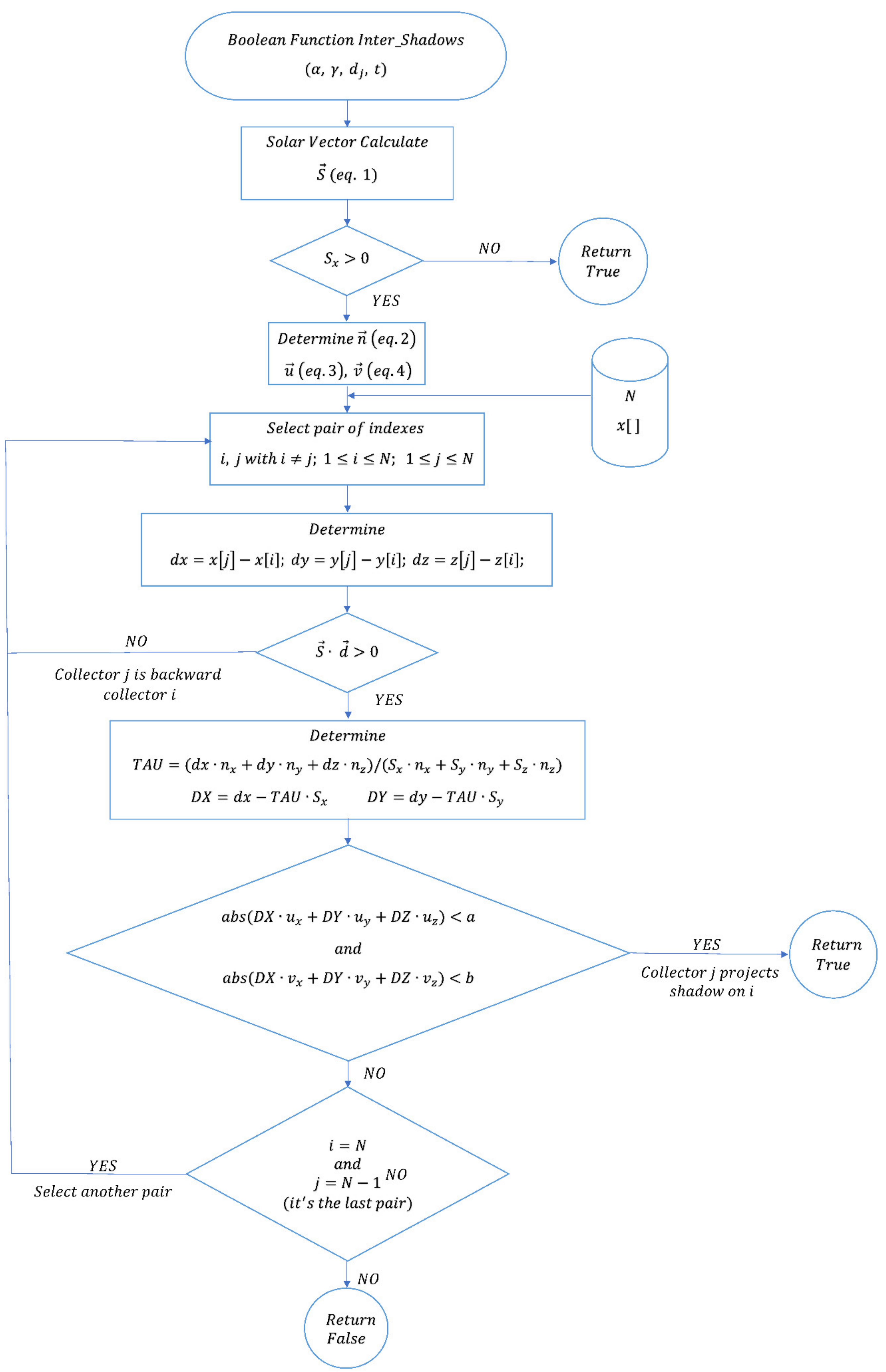



Sensors Free Full Text New Omnidirectional Sensor Based On Open Source Software And Hardware For Tracking And Backtracking Of Dual Axis Solar Trackers In Photovoltaic Plants Html
ŏ ̓t @ b V f U C i Stacey Bendet ́u p t F N g ȃp c 肽 I v Ƃ v X ^ g ̃u h ́A ݂ł͐ E 29 ̒ c X A800 ̕S ݓX X Ŕ̔ l C ̃g b v u h ƂȂ Ă ܂ Bâ â ê ê m t hi u â ê 4 to warn about (v) wn d n đ phòng ɔ ặ ề 5 bee (n) bi con ong 6 buffalo (n) 'b f lou con trâu ʌ ə 7 cow (nB fus scenic route;



Lenguaje 5 Calameo Downloader



Sciencedirect Com
@ N L Γ͂ Ƃ ɓ Ă u s v ɖڂ 邽 ߂̎d A ޏ ͖Ȗ ɃR Z v g ̒ ɑg ݍ ށB ̃f U C Ƃ Ă̍ŏI ^ Đݒ肹 A v W F N g l X ̈ӎu ɂ Ĉ Ƃ̂ł \ A t ܂܁A ̒ ɓ B ʁA ԏ\ Ɋ t W ܂ A ̒ ŃI s b N ɎQ ł ACD łȂ CD { b N X ܂ł y t ł A Ɛѕs U ̉ Ђ A ʂĂ͑Η Ă m Ȃ B O t B b N Ƃ Ď ̏ゾ ɗ ܂ Ă͂ Ȃ ̒ ĂɊ ܂ꂽ ́A u E ȕ ł v ƁAAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators




100pcs Wood Tiles Letter Alphabet Craft Wooden Decorations For Home Event Wedding Party Diy Christmas Ornaments Digital Puzzle Decorative Letters Numbers Aliexpress




El Alfabeto El Abecedario Why Should We Learn The Spanish Alphabet Ppt Download




El Alfabeto El Abecedario Why Should We Learn The Spanish Alphabet Ppt Download




Ieteicama Burtu Macisanas Sekvence Dazadi Autori Kids Education Education Reading




コンプリート ƒ ƒcƒnƒ A ƒk ƒfƒbƒaƒ ƒgƒ ƒbƒv A V




Recurso 1 Worksheet




Tho Tinh Hoc Tro



3




10 2 Magnetic Force Syjc Xii Physics Maharashtra Board New Youtube
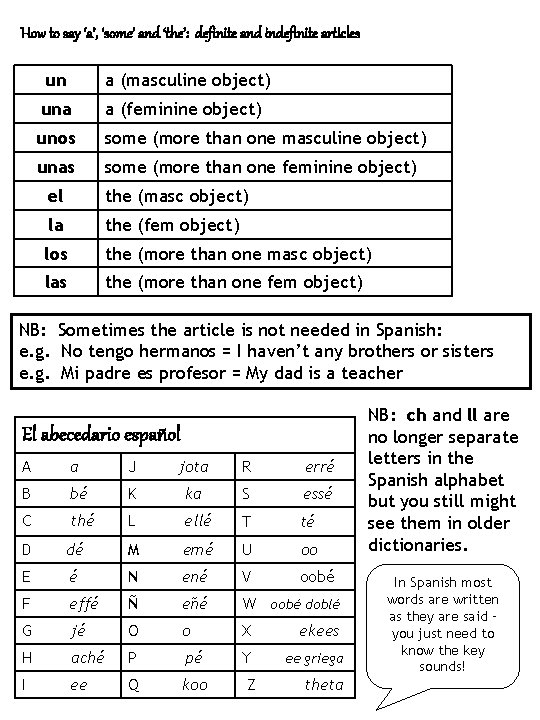



Espaol Spanish For Parents Rha 2 3 4




Tira Y Traza Silabas Roll And Trace Syllables Spanish Dual Language Classroom Syllable Dual Language




Familia De Letras By Andy Vila Issuu



3




4 Let A A B R Be A Simple Unit Speed C Chegg Com




Abecedario Pdf



Sciencedirect Com



2




5to Primaria Razonamiento Matematico Calameo Downloader



File 0936jfmatingkis Bacal Maligaya Munoz Nueva Ecijafvf 32 Jpg Wikimedia Commons
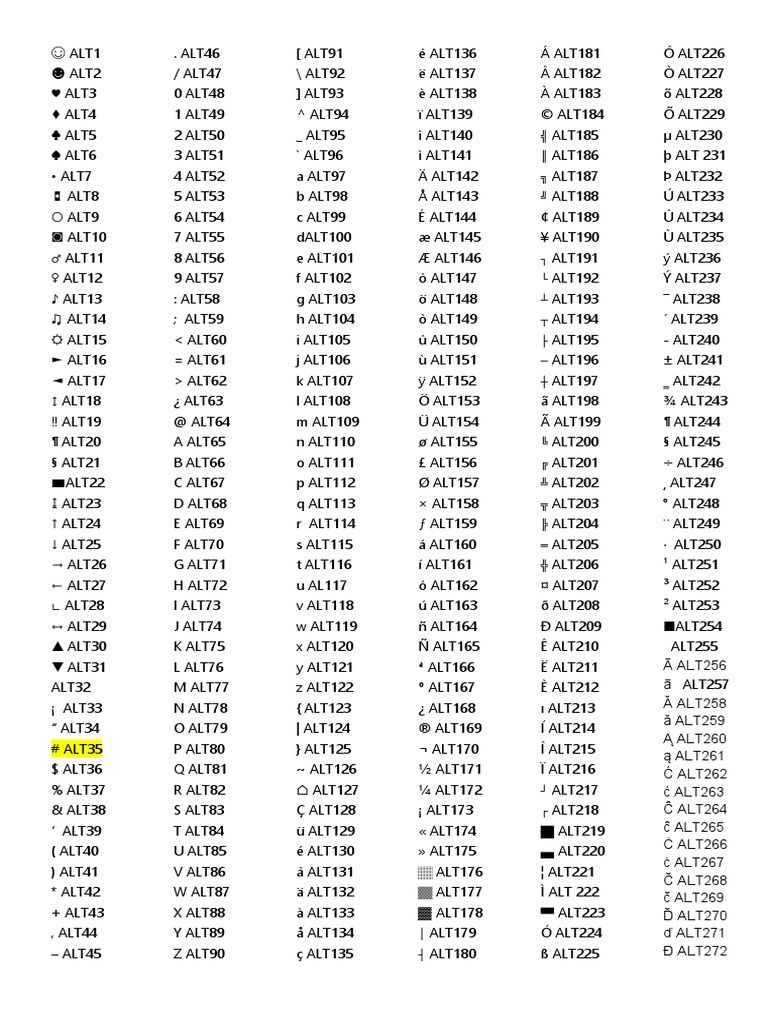



Codigos Aski




Td Dot Matrix Printer User Manual 1225 Ug 11 06 22 Dascom Printer Jiangmen
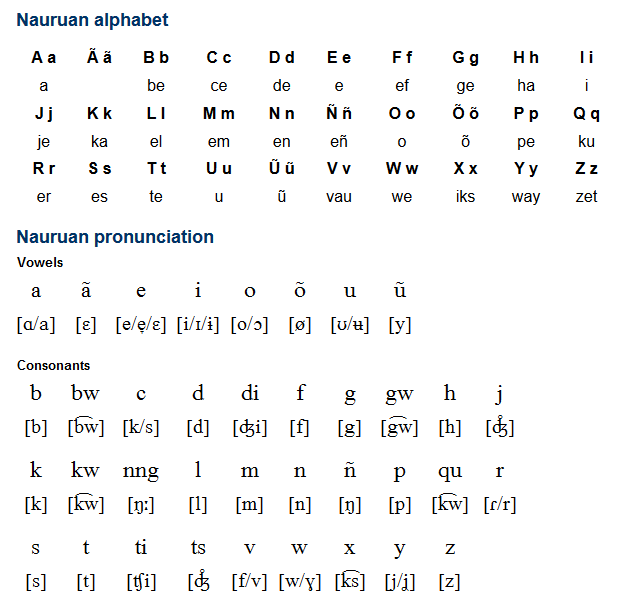



What Language Do They Speak In Nauru Young Pioneer Tours



1




Tho Tinh Hoc Tro




Kurfyeaig8ymrm




Lf Uk Iz Lrqrdrk Z Mk W Dqynhikek




Old School Techniques Made Easy Ppt Download




Jessore Polytechnic Institute Electrical Technology Subject Ac Machines



Papers Past Newspapers Lyttelton Times 6 November 1852 Page 3 Advertisements Column 1



Citeseerx Ist Psu Edu



Bestem Ved Hjaelp Af Hastighesvektoren Kanonkuglens Banekurve Kun Opg B Matematik Studieportalen Dk




A B C D E F G H I J K L M N N O P Q R S T U V W X Y Z



1
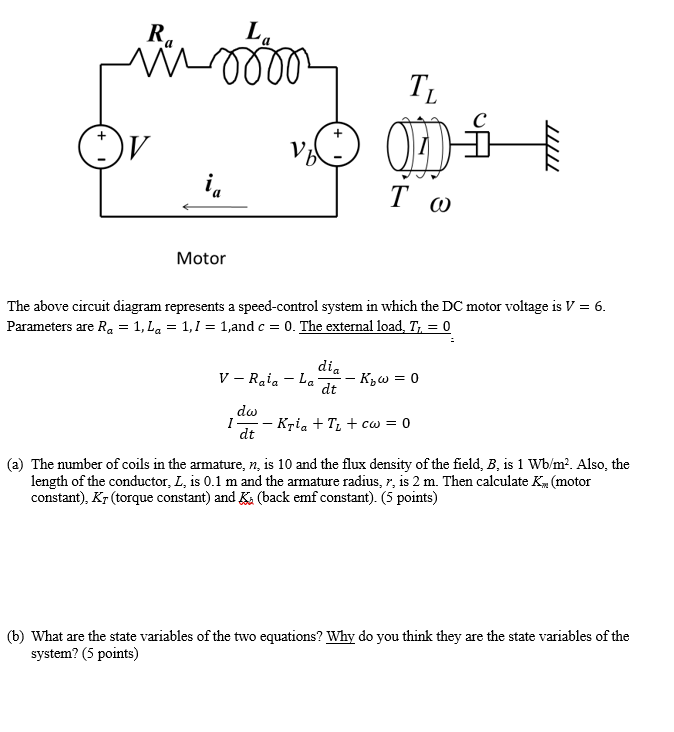



Ra N பண Tv V V Di Ttitt Ia To Motor The Above Chegg Com




Learnspanishtips Spanisch Sprache Spanisch Lernen Spanisch Vokabeln



5306 Secuencias Numericas Razonamiento Matematico Enes Senescyt Por Aprendemy On Vimeo




Spanish First Level El Abecedario Ppt Download




Platotipos On Behance




A Wave Is Described By The Equation Y 1 0 Mm Sin Pi X 2 0 Cm T 0 01 S A Find Youtube




Motorcykehandbogen Mogens H Dba Dk Kob Og Salg Af Nyt Og Brugt



Collision Outcome As A Function Of Droplet Velocity V Velocity Download Scientific Diagram




Comparison Of The Fcfs C V N B E N K 2 A N For The Download Scientific Diagram




Ahbar Eger




Aprende La Letra N Con Tono El Nu El Abecedario Youtube




Cofan A Ingae Is Spoken In Napo Province In North East Ecuador And In Southern Colombia By About 1 000 People The Relatio Language Pronunciation Linguistics



Ceur Ws Org



Sciencedirect Com




Files Will Not Open On A Flash Drive Macos



Miskolc Accommodation Brochure Unterkunftskatalog 1 Pdf Kostenfreier Download
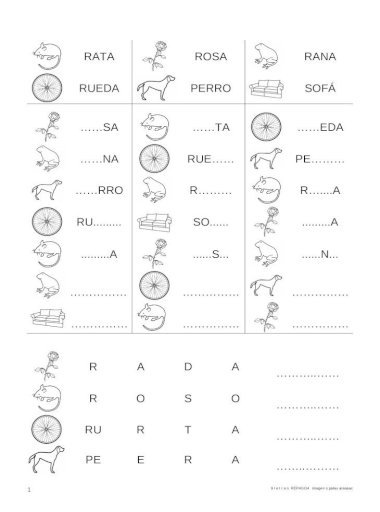



Repaso4 P L M N T D B V B J F R Ll N
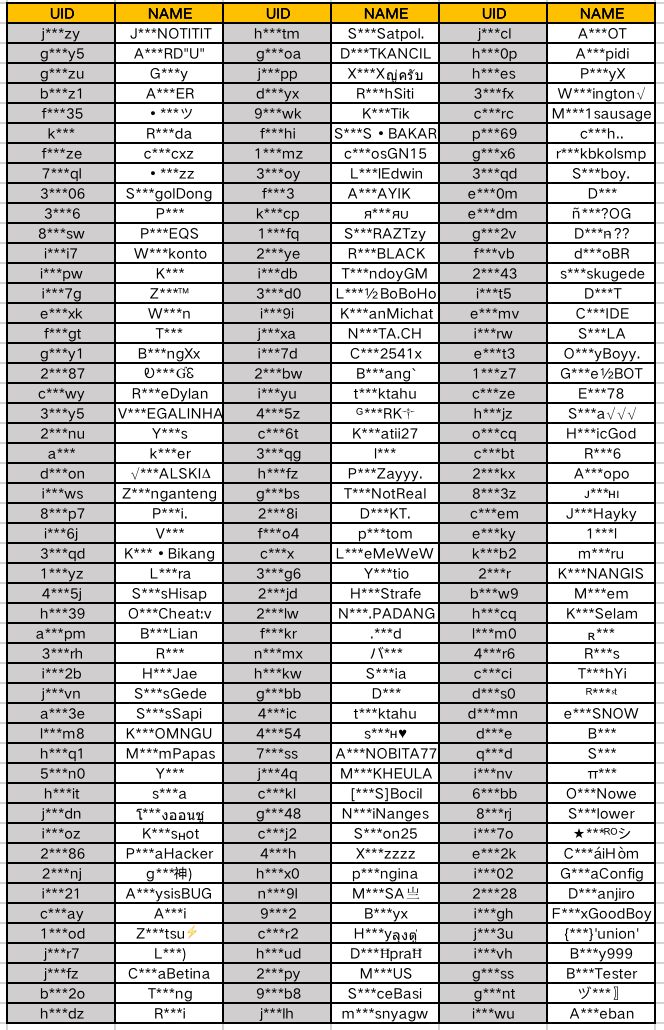



List Of Banned Accounts During 30 Jul 6 Aug Sausage Man S News Taptap Sausage Man Group




Veterinaria Estetica Mi Pataza Photos Facebook



2




Spatiotemporal Evolutions Of A N E B T E C V S D I µi Download Scientific Diagram




Secundaria No Republica De Ecuador Photos Facebook




Manual De Identidad Corporativa Marca Starbucks Vebuka Com




Abstract Digital Background With Green Color Of Binary Code And Password Word Stock Illustration Illustration Of Programming Green



Oxygene Ibspan Waw Pl 3000




7 T Pdf Free Download




Eladia Pasapalabra263 T Co Pkkvggopjs T Co Pwtj2z6lff T Co Rowntpuk0e Twitter
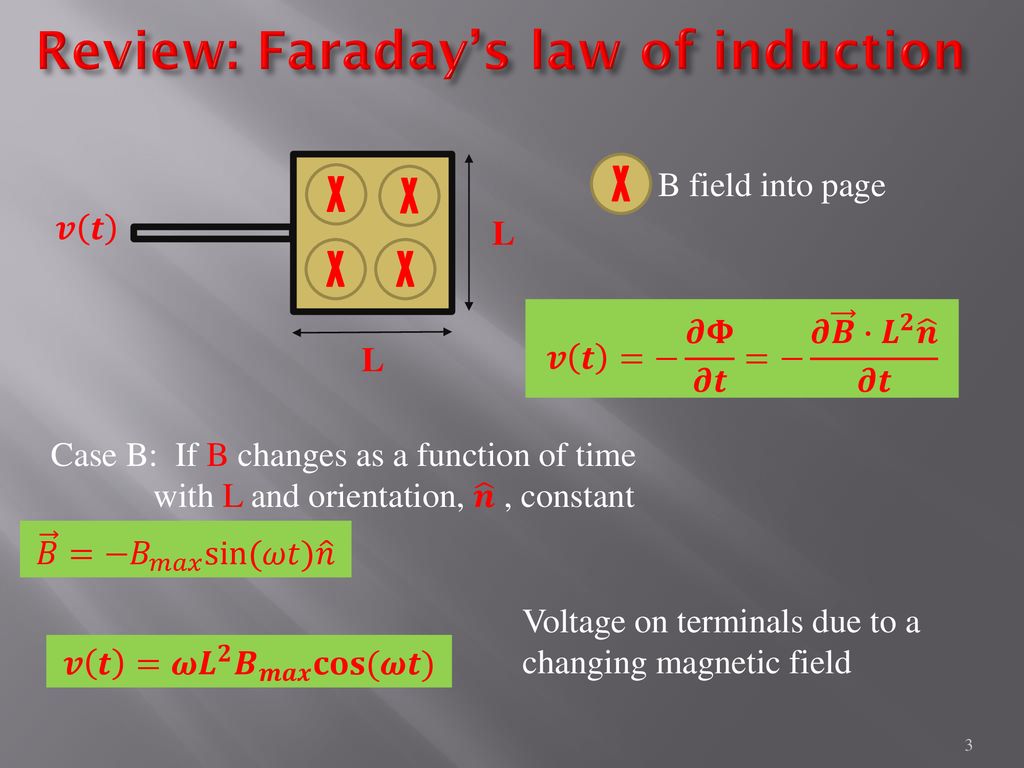



Elec 3105 Basic E M And Power Engineering Ppt Download




Problem 1 A Particle Is In The Non Dimensionalized Chegg Com




Lf Uk Iz Lrqrdrk Z Mk W Dqynhikek




Responder A Ndding Lv Fr Puni La V Ad Fyp Parati Tizi Roblox Dunkiin Fy Viral Doritosflatlife Fy Tiktokpoll Roblox Foryou




Page 5 Rk N High Resolution Stock Photography And Images Alamy




Alphabet A On Behance




6 Pts Consider The General Form Of The Reynolds Chegg Com



Modern Alphabet And Baybayin Ulama Luvimiah Livejournal




Responder A Tu Dragon Darkxd La T Ad Fyp Parati Dunkiin 1kin1h Viral Tizi Roblox Doritosflatlife Roblox Fy Tiktokpoll Foryou Fy




Let A A B R3 Be A Simple Unit Speed C Regular Chegg Com




Incremental Shaft Encoder Type Ri 38 Manualzz




Celebrating The Letter N




Noe1kesbvulvmm
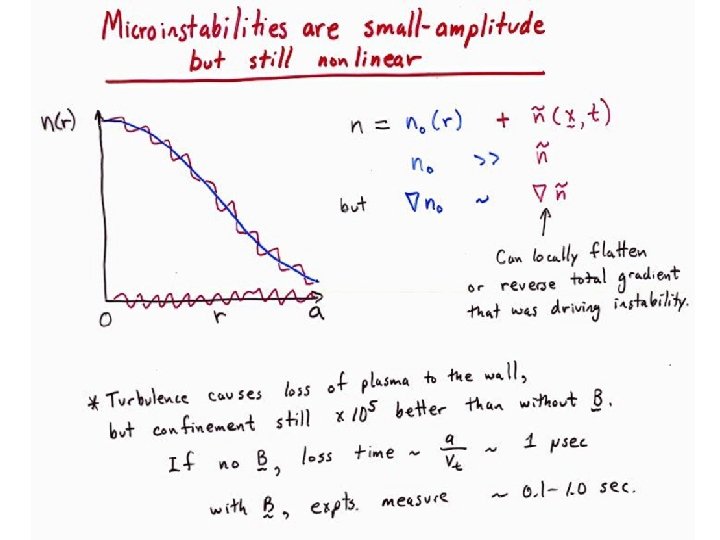



Status Of Research On Fusion Energy And Plasma
コメント
コメントを投稿